artifax
artifax is a Python package to evaluate nodes in a computation graph where
the dependencies associated with each node are extracted directly from their
function signatures. Here’s an example of artifax in action:
>>> from artifax import build
>>> import math
>>> build({
... 'x': math.pi/3,
... 'sin': lambda x: math.sin(x),
... 'cos': lambda x: math.cos(x),
... 'y': lambda sin, cos: 2*sin - 1.2*cos
... })
{'x': 1.0471975511965976, 'sin': 0.8660254037844386, 'cos': 0.5000000000000001, 'y': 1.132050807568877}
Install with pip:
$ python3 -m pip install artifax
A computation graph can be entirely encoded in a standard python dictionary. Each key represents a node or an artifact, that will eventually be computed once all of its dependencies have been calculated. The value associated with each key can be either a constant - a string, a number or an instance of a class, or a function. In the latter case, the function arguments map to other nodes in the computation graph to establish a direct dependency between the nodes.
For example, the following dictionary:
artifacts = {
'A': 42,
'B': 7,
'C': lambda: 10,
'AB': lambda A, B: A*B,
'C-B': lambda B, C: C - B,
'greeting': 'Hello',
'message': lambda greeting, A: '{} World! The answer is {}.'.format(greeting, A)
}
yields the following computation graph:
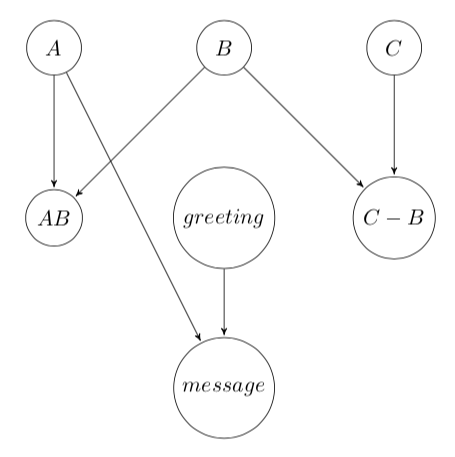
The build function evalutes the entire computation graph and returns a new dictionary
with the same keys as the original one and with the calculated values for each of the nodes
in the computation graph.
from artifax import build
artifacts = {
'A': 42,
'B': 7,
'C': lambda: 10,
'AB': lambda A, B: A*B,
'C-B': lambda B, C: C - B,
'greeting': 'Hello',
'message': lambda greeting, A: '{} World! The answer is {}.'.format(greeting, A)
}
result = build(artifacts)
for k, v in result.items():
print(f"{k:<10}: {v}")
outputs
A : 42
B : 7
C : 10
AB : 294
C-B : 3
greeting : Hello
message : Hello World! The answer is 42.
Artifax class
The build function represents the core transformation that yields artifacts.
It is entirely stateless and has no side-effects. Given the same input graph, it will always
evaluate every single node and generate the same results.
Whilst these features are highly desirable from any core component, the stateful Artifax
class can be employed to interface with the build function and provide some additional features
and performance enhancements.
from artifax import Artifax, At
def double(x):
return x*2
afx = Artifax()
afx.set('a', 42)
afx.set('b', At('a', double))
# set also accepts named arguments
afx.set(c=lambda b: -b)
assert len(afx) == 3
assert 'b' in afx
results = afx.build()
for k, v in results.items():
print(k, v)
# c -84
# a 42
# b 84
Lazy builds
Artifax instances optimize sequential builds by only re-evaluating nodes that
have become stale due to an update. For example, given the graph illustrated in
Figure 1, if node B is updated, e.g, afx.set('B', -5)), nodes B, AB and
C-B get re-evaluated when the build method is invoked, but not any other
nodes.
In the example below, the second call to the build method triggers a
re-evaluation of node p1 and all the nodes that depend on it. Nodes v2 and
m2, on the other hand, do not require re-evaluation since they do not depend
on the updated node.
import artifax
import math
class Vector:
def __init__(self, u, v):
self.u = u
self.v = v
def magnitude(self):
print('Calculating magnitude of vector {}...'.format(self))
return math.sqrt(self.u**2 + self.v**2)
def __repr__(self):
return '({}, {})'.format(self.u, self.v)
afx = artifax.Artifax(
p1=(3, 4),
v1=lambda p1: Vector(*p1),
m1=lambda v1: v1.magnitude(),
v2=Vector(5, 12),
m2=lambda v2: v2.magnitude()
)
_ = afx.build()
print('Updating p1...')
afx.set(p1=(1, 1))
_ = afx.build()
Calculating magnitude of vector (3, 4)...
Calculating magnitude of vector (5, 12)...
Updating p1...
Calculating magnitude of vector (1, 1)...
Targeted builds
The build method accepts an optional argument that specifies which node in
your computation graph should be built. Instead of returning the usual dictionary,
targeted builds return a tuple containing the value associated with each of the
target nodes.
terminal_node_value = afx.build(targets='terminal_node')
some_node, another_node = afx.build(targets=('node1', 'node2'))
Targeted builds only evaluate dependencies for the target node and the target node itself. Any other nodes in the computation graph do not get evaluated.
from artifax import Artifax
afx = Artifax({
'name': 'World',
'punctuation': '?',
'greeting': lambda name, punctuation: 'Hello, {}{}'.format(name, punctuation),
})
greeting = afx.build(targets='greeting')
print(greeting) # prints "Hello, World?"
afx.set('punctuation', '!')
greeting, punctuation = afx.build(targets=('greeting', 'punctuation'))
print(greeting) # prints "Hello, World!"
print('Cool beans{}'.format(punctuation)) # prints "Cool beans!"
Targeted builds are an efficient way of retrieving certain nodes without evaluating the entire computation graph.
Solvers
Depending on the use case, different solvers can be employed to increase performance.
The build function and methods accept an optional solver parameter which defaults to
linear.
The linear solver
The linear solver topologically sorts the computation graph to define a sequence of nodes to be calculated in an order such that for any node, all of its dependencies appear before in the sequence.
The parallel solver
The parallel solver consumes the computation graph starting from the nodes that have
no dependencies and processes them all in parallel. When this initial set of nodes is resolved,
their immediate neighbors make up the new frontier which also gets processed in parallel.
This procedure continues until there are no more nodes to be calculated. At any step, the
solver spawns one new process for each node at the frontier without exceeding the number of
available cores minus 1.
The async solver
The async solver takes the parallelism of the parallel solver one step further. It is triggered
each time a node evaluation is completed, looking for new nodes that can be started and evaluating
them in a new process immediately.
Error handling
If the computation graph represented by the artifacts dictionary is not a DAG
(Direct Acyclic Graph), a CircularDependencyError exception is thrown.
import artifax
try:
_ = artifax.build({'x': lambda x: x+1})
except artifax.CircularDependencyError as err:
print('Cannot build artifacts: {}'.format(err))
Cannot build artifacts: artifact graph is not a DAG
If a particular node is represented by a function for which any of its arguments isn’t part
of the computation graph, an UnresolvedDependencyError exception is thrown.
_ = artifax.build({
'x': 42,
'p': lambda x, y: x + y
}) # raises UnresolvedDependencyError due to missing 'y' node
However, sometimes this behavior might be desirable if we want nodes to resolve to partially
applied functions that can be used elsewhere. If that’s the case, the exception can be suppressed
by setting the allow_partial_functions optional parameter to build to True.
results = artifax.build({
'x': 42,
'p': lambda x, y: x + y
}, allow_partial_functions=True)
print(results['p'](100)) # prints 142
